Turing Complete: The 'Condition 10' Achievement
The ‘Condition’ level in Turing Complete
I recently re-started playing the computer-science game Turing Complete, where your job is to build and program a computer from scratch, starting with simple logic gates like AND, OR or NAND, and successively building more complex components until we have a functioning computer.
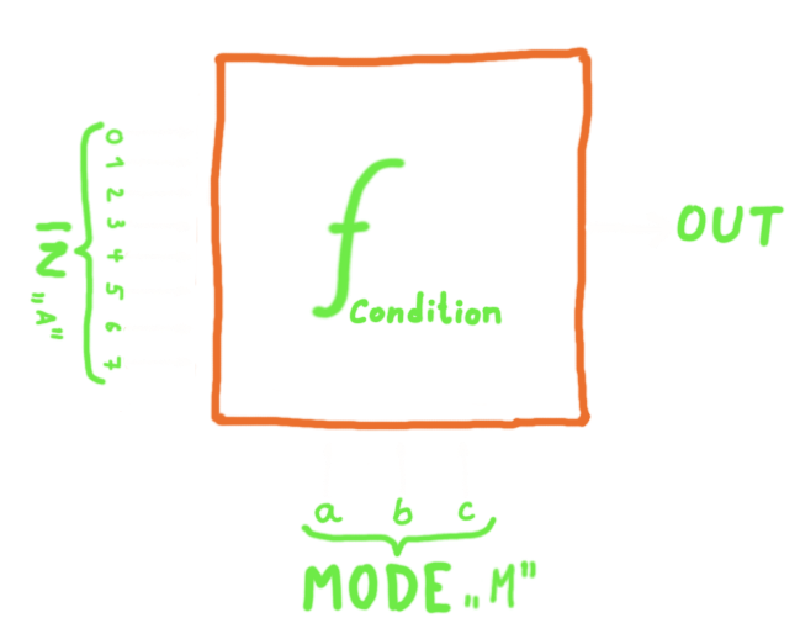
The objective of the Condition level is to create a comparison unit. Such a
unit takes a byte A and a mode M (3 bits) and calculates the output according
to the mode as
| mode | output | in short |
|---|---|---|
| 0 | always 0 | 0 |
| 1 | 1 if A is equal to zero | =0 |
| 2 | 1 if A is less then zero | <0 |
| 3 | 1 if A is less or equal to zero | <=0 |
| 4 | always 1 | 1 |
| 5 | 1 if A is not zero | !=0 |
| 6 | 1 if A is greater or equal to zero | >=0 |
| 7 | 1 if A is greater then zero | >0 |
Our job is to find build the function f according to the above description.
The naive solution
The straightforward approach is to calculate the various conditions and route
the desired one to the output, depending on the setting of M, the mode:
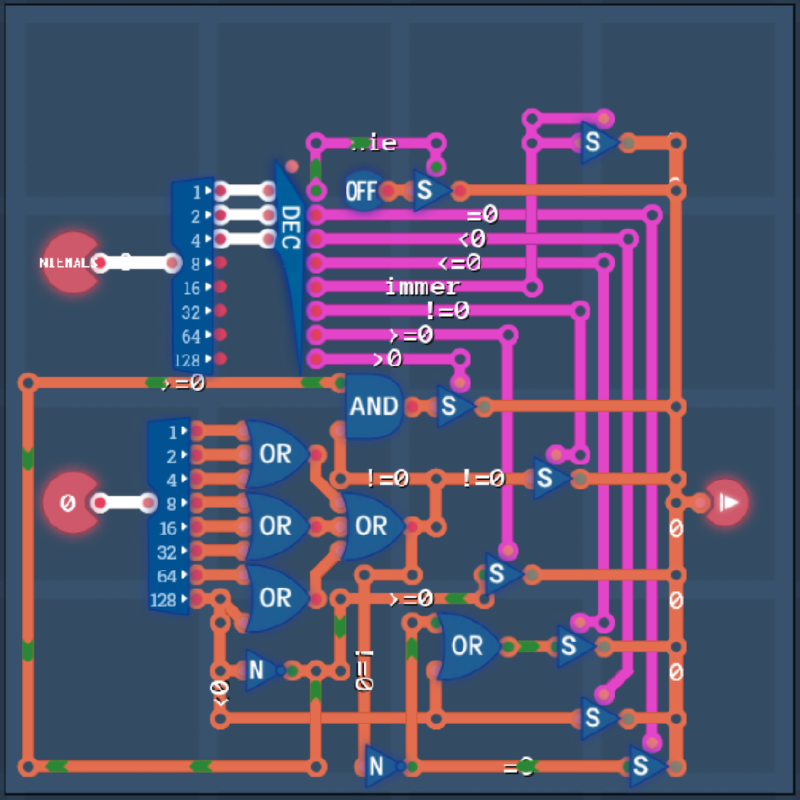
So far so good, another job well done. But then the Condition 10 achievement, to solve the condition level with only 10 blue parts caught my attention:

Looking at the naive implementation, it is immediately clear that this is not achievable with just some clever micro-optimizations. We need a different approach here that drastically reduces the count of blue components used.
Reducing complexity
Let’s start with the observation, that all required conditions can be reduced
to expressions only using =0 (called z like zero in the following) and
<0 (called n like negative):
| mode | output | calculate as |
|---|---|---|
| 0 | 0 | 0 |
| 1 | =0 := z | 1 if all bits of A are 0 |
| 2 | <0 := n | bit 7 (sign bit) of A |
| 3 | <=0 | z ∨ n |
| 4 | 1 | 1 |
| 5 | !=0 | ¬z |
| 6 | >=0 | ¬n |
| 7 | >0 | ¬z ∧ ¬n |
Conceptually, we can redesign the circuit as follows: first calculate n and
z from the input value A, then calculate the final output as a 5-ary function
f of n and z and the mode as a, b, and c. Therefore we need to set
up the truth table for f and then synthesize a logic function that evaluates
f.
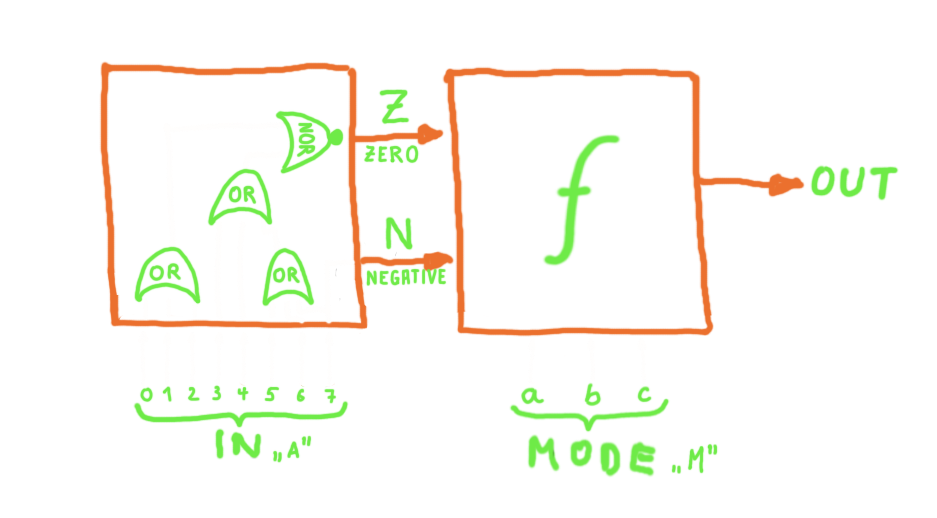
Reducing the problem to 5 variables, n and z and the mode as three bits
a, b and c (where a is the least significant bit), yields this truth
table:
| n | z | c | b | a | out |
|---|
Looking at the table, we see that c divides the table into two complementary
parts with f(c=1) = ¬f(c=0). This property is key to the presented
solution.
Recap: XOR as a controllable inverter
One interesting property of XOR (⊕), that helps in understanding the next step,
is, that XOR can be interpreted as a NOT-gate that can be enabled or
disabled. If disabled, the output is the input as-is. If enabled, the output is
the inverted input. This becomes immediately clear if we name the two inputs of
XOR as INVERT, which controls the negation, and the actual INPUT, which is
negated, or not:
| INVERT | INPUT | OUTPUT |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Simplifying f
With f(c=1) = ¬f(c=0) we now can rewrite f to: f = g ⊕ c or
f(n,z,a,b,c) = g(n,z,a,b) ⊕ c, reducing the problem to finding the 4-ary
function g of:
| n | z | b | a | out |
|---|
Looking at the highlighted cells, we see that g(n,z,b,a) is 1 if a ∧ z
is 1 or if b ∧ n is 1, resulting in g(n,z,b,a) = (a ∧ z) ∨ (b ∧ n).
(In a systematic approach, we would calculate all 6 possible AND combinations
of n, z, a and b, e.g. a ∧ b, a ∧ z, a ∧ n and so on. Then
we would check which term covers which rows. Finally we would find out that only
a ∧ z together with b ∧ n covers all rows where the output is 1)
Putting it together: the condition component with only 10 blue parts
Subsituting g in f = g ⊕ c results in f(n,z,c,b,a) = ((a ∧ z) ∨ (b ∧ n)) ⊕ c.
Finally we can wire up our condition component with only 10 blue parts
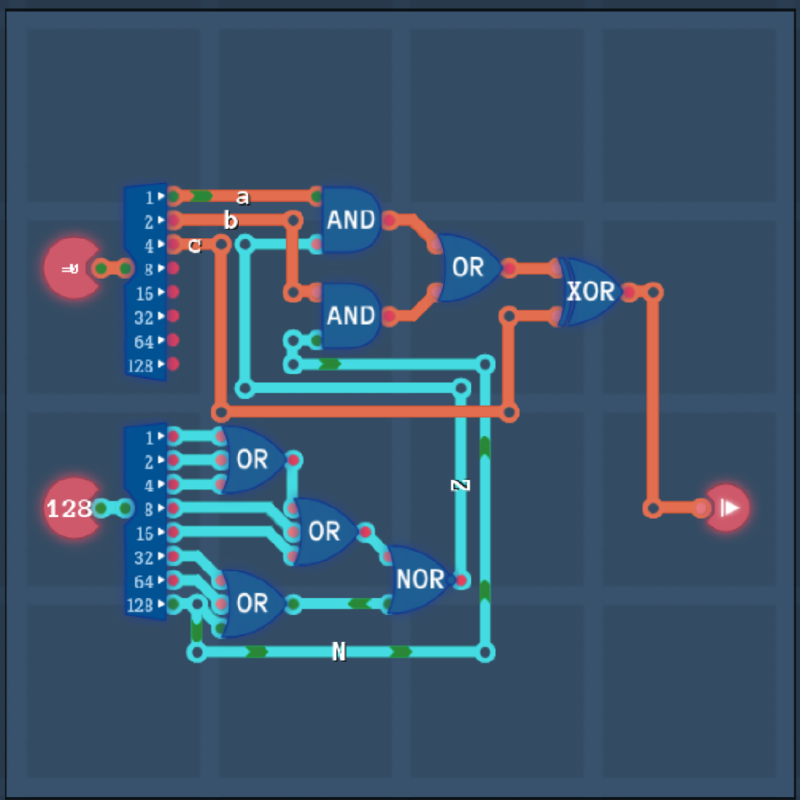
and earn the achievement.

